Text
The God of Irreducible Complexity
What should Christians think about the central claims and implications of chaos and complexity theory?
By Noel Weichbrodt
For me, the study of chaos theory was not the the triumphant Waterloo of indeterminism over the modernist forces of determinism. That honor and ignominy belongs to Gödel’s Theorem, where my faith in mathematics as a complete description of the world fell to a little Belgian and his elementary number theory. Chaos could have done the same thing to me, though. A case for chaotic systems being the fundamental way our world works, made in the book Chaos: Making a New Science by James Gleick, levels a similar blow as Gödel’s Theorem against determinism.
Reading the book is truly an eye-opening experience. The way you see reality, and specific events, is completely altered. Staring at the waves along the South Carolina shoreline becomes a meditation on the irreducible complexity of the ocean. Watching smoke lazily spiral upward, you recognize the same patterns that you saw mixing creamer into your coffee, which in turn are similar to haunting pictures of the Mandelbrot set. Staring at a waterfall, you begin to meditate on the aperiodicty of the streams coming down, while at the same time noticing subtle patterns in the wash that come and go as they please. Is the world truly chaotic? Perhaps before that may be answered, we should understand what chaos is.
First, I want to examine on a highly conceptual, non-mathematical (and thus non-rigorous) level the five central tenets of chaos. Then, I will share a bit regarding how I think Christians should respond to the tenets and implications of chaos theory. To give away the show, I think that Christians should accept chaos theory and take from chaos theory a renewed humility regarding our noetic ability. There is an impressive array of evidence for chaos, and the theory is compatible with our Christian metaphysic. The study of chaos brings you bowing before the throne of grace to the triune God whose creativity, incomprehensibility, and beauty are made manifest in nature.
The similar patterns that appear in your coffee, in your fireplace, and in the Mandelbrot set denote the first central idea of chaos: patterns repeat on many scales.1 This tenet comes by way of fractals, objects which have a fractional dimension (say, 1.2618 for the Koch Triangle2). The idea is, you see the same patterns repeated across scales and systems. Repeating patterns across scales means that you can see the same repeating elements (patterns) whether you are zoomed in 10,000% or zoomed out 1%. The Koch triangle is a good example of this: the same shapes appear no matter how closely you look at it. Repeating patterns across systems means that you notice similar shapes (patterns) in different objects. For example, the branching of a tree, and the branching of human blood vessels look similar, even though they are completely different pieces of creation.3
Checking the forecast two weeks ago, I had expected this weekend to be sunny and in the 80s, not 60 and raining like it is right now. Why is long-term weather forecasting so difficult? Chaos theory posits that the weather, among other systems, has an infinite sensitive dependence to initial conditions.4 This means that to accurately predict (forecast) what the behavior of a chaotic system will be, you must know the initial starting conditions of the system down to an infinite, and thus unobtainable, degree. For long-term weather forecasting, that means the meteorologist must know what the infinitely exact temperature is at every single point in space for the entire world—an impossible endeavor! Even a small change in a variable, say the difference between 21.9999999995 and 21.9999999996, results in a system behaving unpredictably. This tenet is often referred to as the Butterfly Effect: the flapping of a butterfly’s wings in the Amazon causes a tornado in Oklahoma.
Watching those waves roar onto shore, I realized two things: the ocean is a complex, chaotic system, and (this is the third tenet of chaos) complex systems are irreducibly complex. By irreducibly complex, I mean that the only way to model that system is to create an entirely new system, exactly the same in every detail. Combine that new system with the second tenet, sensitive dependence on initial conditions, and you will realize that the second and third tenets imply that creating that new system is impossible. If you want to model the ocean exactly, you must create an entirely new ocean, exactly the same down to an infinite level of detail, which can never be reached, much like Zeno’s tortoise will never finish the race. Trying to abstract out the ocean will never capture the full complexity of the system. I think most of us already knew that, but for various reasons hold the belief that our abstractions capture the main points, and that the minor details are irrelevant. Chaos, in the third tenet of irreducible complexity, claims that even the minor details are vital—to lose them is to lose grasp of the system. Perhaps that explains why our abstractions fail as often as they succeed.
Edward Lorenz in 1961 developed a simple, four-equation system that modeled four key parts of the weather. That four-equation computer simulation, to his delight, displayed unpredictable, aperiodic, chaotic behavior. The fourth tenet of chaos, simple systems display chaotic behavior, notes the same thing Lorenz discovered on his computer printouts. Take a simple water system, like a dripping faucet. Try to predict when the next four drips will occur. Even though there are only a (relatively) few molecules at work in it, you will give up in frustration. That simple system is chaotic, displaying irregular, aperiodic behavior.
If even simple systems are chaotic, then that holds a startling implication (and this is the fifth tenet of chaos): non-linearity describes almost every system in the world. If you don’t believe this, ask your friendly neighborhood physicist. They know that all those equations you learned in high school physics apply to only a very small fraction of the real world.5 We live in a world of chaos, full of irregularity, complexity, and things that we don’t fully understand. Chaos theory tells us to drop our pretenses of having, or even hoping to have, a full, complete knowledge of the world we live in. Not only that, but from tenet four, we should know that any natural system, no matter how simple, is really quite unpredictable.
Chaos theory does not spell the end of science. Part of chaos theory is finding and understanding those irregular, aperiodic patterns. You may not be able to predict the weather a month from now, but you can make a pretty good shot at next week. Even in the most chaotic systems there are islands of regularity, where things behave linearly and periodically. The sun rises and sets at certain times—there is order and regularity in the world, no doubt.
These claims and implications of chaos theory are both far-ranging and counterintuitive, or at least counter-rational. However, chaos theory has assembled a wide range of evidence for its claims. Albert Libchaber investigated fluid dynamics and found that flow is indeed chaotic, but has predictable spots of order6 . Chaos theory explains the islands of order and limited movement of Jupiter’s Great Red Spot7 . The changes of weather can only be explained in the context of nondeterministic systems with sensitive dependence on initial conditions8 . The heart is both stable and chaotic, making its pump predictable yet surprisingly resistant to change, while medical conditions such as fibrillation are deadly to the heart for their aperiodicy9. And remember that dripping faucet? Chaotic dynamics both explains why the dripping is aperiodic, and successfully predicts the drip patterns10 .
All these claims and evidences may be hard to swallow. Why is accepting and understanding chaos theory so hard? The biggest problem in accepting chaos theory is that it requires a drastic shift from the standard modernist metaphysics and ontology. The world goes from the modernist idea of deterministic, orderly, and reducible to nondetermenistic, random, and irreducible. At its heart, chaos is a new way of looking at things. You can view nature as the work of a divine watchmaker, filled with predictable cogs and absent a creator. Or you can view nature as a breathtaking display complexity, elusive order, and surprise by an immanent Creator. Perhaps a litmus test could be suggested: when you start to ponder the ocean, do you see a piece of creation that we have conquered and subdued, or do you see intriguing, elusive glimpses of order in waves of chaos?
So, what is a Christian to do with all this? First, I think, we should not be frightened by the loss of modernist ideas about the way the world is and works. Our understanding of the Trinity, as revealed in Scripture, is quite at home in a chaotic world. Of course, God is a God of order—that is why we find order in the world. But that does not mean that He is also an understandable, predictable Creator and Sustainer. That the universe is, in ways we are just beginning to understand, incomprehensible and immeasurable simply reflects the incomprehensibility and immeasurability of its Creator.
Which brings me to my second recommendation of what Christians should take from chaos theory. Our study of nature as chaotic should drive us back to the throne of grace. Even though we cannot grasp all of creation, there is a Creator who not only grasps it, but has made it and called it good. The study of chaos should bring us a renewed sense of humility and wonder. We are finite, and cannot understand everything—even our own hearts!
Finally, I would like to call attention to an idea that Dr. Petcher has put forth: openness in nature. That nature is nondeterminstic (open) is a sign of God’s immanent Spirit-presence in nature. God’s purposes in creation are eschatological, focused on the eventual redemption of creation from the rot of sin. The full meaning of his purposes are not capture in creation, but are at work through his Spirit—in this day, at this very moment. Chaos, perhaps, is God’s Spirit at work in incomprehensible ways, creating and sustaining His creation as we watch, just as the Spirit is creating and sustaining us, His Church.
Appendix One: The Mandelbrot Set
Perhaps one of the most intriuging objects in chaos theory is the Mandelbrot set. From http://aleph0.clarku.edu/~djoyce/julia/explorer.html, I generated these four images. Each image is a section of the previous, magnified 3x.
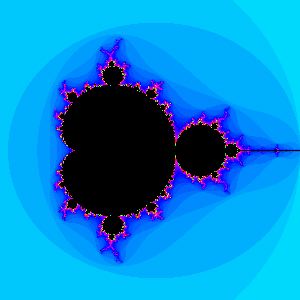 1
1 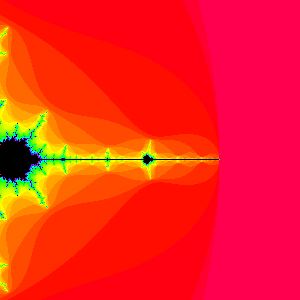 2
2 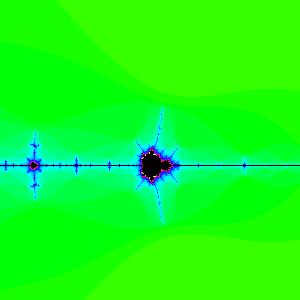 3
3 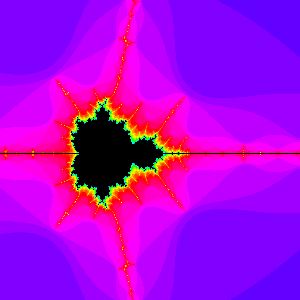 4
4

1 Chaos, p. 109.
2 Ibid, p. 102.
3 For an example of scale similarity, see Appendix One for pictures of the Mandelbrot set, which illustrates many of the tenents discussed in this paper.
4 Chaos, p. 23.
5 My neighborhood physicist, Dr. Donald Petcher, told me that only roughly 1% of systems in the world are deterministic, displaying periodic behavior, and able to be modeled.
6 Chaos, p. 209.
7 Ibid, p. 54.
8 Ibid, p. 23.
9 Ibid, p. 281
10 Ibid, p. 263.